Antoninus
Pius
Marcus Aurelius Antoninus Pius (121
- 180) "hat durch
seine Gelehrsamkeit einen ebenso großen Ruhm erlanget, als durch
seine Regierung, welche insgemein das güldene Zeitalter genennet wird."
Er "lies die Verbesserung des Staats und der Sitten
der Bürger sein beständiges Augenmerk seyn, so daß er den
großen Ruhm hinter sich lies, er habe die schlimen Bürger zu
guten, und die guten zu den besten gemacht. Hierauf sahe er bei allen seinen
Reisen, zu welchem Endzwek er Künste und Wissenschaften beförderte,
Schulen anlegte, öffentliche Lehrer bestellte, und sie mit Einkünften
versahe, wie diese Vorsorge besonders Athen genossen hat."
Auf die Berichte über seine Reisen (nach Syrien und Ägypten)
nimmt Gerhard Mercator hier wohl Bezug. In seinen 12 Bücher
(meditationes) de se ipso, seu vita sua,
von Guil. Xylander 1558 bei
Andreas
Gesner in Zürich herausgegeben, ist von seinen Reisen nicht die
Rede. Wo das Itinerarium Antonini zu
finden ist, habe ich bis dato
nicht herausfinden können. Mercators Exemplar - hgg. von Heinrich
Stephan, wann?, wo? - war in seiner Bibliothek (vgl. den Catalogus
librorum bibliothecae1604, S.21)
zusammengebunden mit Pomponius Mela [?De
situ orbis] , Julius Solinus [?De
situ orbis terrarum & memorabilibus, quae mundi ambitu continentur
liber, ?De mirabilibus mundi]
u.a. "cum annotationibus marginalibus".
coma berenices
Berenice (um273-221
v.Chr.) war Königin im alten Syrien und Ägypten. Sie war die
Tochter und Nachfolgerin des Königs Maga von Syrien. Im Jahre
247
heiratete sie Ptolemäus III. und vereinigte damit erfolg- und
folgenreich die Regentschaft von Syrien mit der von Ägypten.
Sie schnitt sich ihren wallenden Haarschopf (coma berenices), um ihn
für die sichere Rückkehr ihres Gatten aus dem Krieg auf dem Altar
der Götter zu opfern.
Folgen wir Callimachus und Catull, so benannte der sicher
aus dem Krieg heimgekehrte Ptolemäus III. ein Sternbild nach
der Opfergabe seiner Gattin: Coma Berenices.
Mercator: Cincinnus = Das gekräuselte
Haar = Berenicis crinis = Das Haar der Berenice
Antinous
Kaiser Publius Aelius Hadrianus (76-138)
war dem jungen Antinous - geboren um 111
in Claudiopolis - offenbar derart in homo-erotischer Beziehung verbunden,
daß die Beziehung Beider der mythologischen Beziehung zwischen Zeus
und Ganymed gleichgestellt wurde.
 |
Als der junge
Antinous132 auf tragische
Weise im Nil umkam, versank Hadrian nahezu in Umnachtung. Im Traum
scheint ihm der Tod des Antinous als Aufstieg zu den Göttern
vorgekommen zu sein, so daß er Antinous kultisch "zur
Ehre der Altäre" erhob und ihm kurz nach seinem Tod - noch in 132
- ein Sternbild - heute als Teil des Sternbildes Aquila angesehen
- zuordnete. |
[1]DE USU
Die Überschriften sind von J. van Raemdonck aus dem Text
Mercators
abgeleitet worden. Ich gliedere den Text in die Hauptteile
-
III Über [einige Probleme und]
den Gebrauch des Erdglobus
[Für den ersten Teil ist die Überschrift
Raemdoncks
zu kurz gefaßt, da er sowohl Aussagen über den Gebrauch
des Globus als auch die Darstellung bzw. die Mitteilung einiger
Probleme an Kaiser Karl V. enthält.]
-
III Über den Gebrauch des Himmelsglobus
-
III Über den Gebrauch des Astronomischen Rings
Ad I: In wesentlichen äußert sich Gerhard Mercator
(1) über seine magnetischen Studien - im Zusammenhang
damit -
(2) über die (längst ad acta gelegte) Moluccenfrage
-
(3) über die Korrekturen, die an der Kartierung Europas
nach Ptolemäus anzubringen sind, sowie - daraus schlußfolgernd
-
(4) über seine Erkenntnis, daß der Nullmeridian durch Corvo
nicht durch Neu-Indien hindurchgeht.
(I.1.1) Mercator wiederholt seine spätestens
mit dem 1546er Brief an den Bischof
von Arras ?bekanntgewordene Ansicht über die prinzipielle Lage
des magnetischen (Süd-)Pols - der Brief wurde erst 1869
durch Breusing allgemein bekanntgemacht - , diskutiert dann
aber seine konkrete Lage unter - nach 1546
- veränderten Gesichtspunkten..
(I.1.2) Da er alle seine erdmagnetischen Überlegungen unter
das Axiom von den Isogonen (als Großkreisen) stellt,
kommt er jetzt zu zwei - vorher noch nie und nirgends gemachten - Vorschlägen:
(a) wie man den Längengrad eines Ortes mit Hilfe
der Kompaß-Mißweisung am betreffenden Ort findet und
(b) wie man - umgekehrt - die Kompaß-Mißweisung an einem
Ort mit Hilfe des Globus findet.
Axiom von den Isogonen: Iso-Linien sind
Kurven gleicher Meßwerte in einer Kurvenschar; Isogonen sind Kurven
gleicher magnetischer Deklination, Isoklinen sind Kurven gleicher magnetischer
Inklination.
William Gilbert konnte sich (1600)
die magnetischen Eigenschaften des loadstone's
bzw. der mit ihm bestrichenen needle
nur durch das Modell von der Erde als Magnet selbst erklären.
Erst J. Tobias Mayer (1760),
J.
Heinrich Lambert (1766), C.A. Coulomb (1785)
näherten sich einer mathematischen Theorie des Magnetismus, die dann
1832/33
in der Arbeit von C.F. Gauß über die Intensitas
vis magneticae terrestris ihren (ersten) Abschluß
und Höhepunkt fand.
[2]Erforschung
Die beiden ersten Abschnitte rekapitulieren die Argumentation des Briefes,
den Gerhard Mercator am 23. Februar 1546
an den Bischof von Arras geschrieben hatte. In diesem Brief diskutiert
er die Lage des Poles mit Bezug auf die Zeichenfehler, die ihm beim Studium
diverser Karten der Küste Kanadas aufgefallen waren: mal fielen in
diesen Karten die Breitendifferenzen zu klein, mal zu groß aus. Da
ihm schon die Küsten Afrikas - in den Karten ptolemäischer Tradition
- Kummer gemacht hatten (s.w.u.), erkennt er nun - cepi
ego diligentius errorum causas perquirere, potissimamque inveni in magnetis
ignorata conditione consistere - , daß die Fehler in den Seefahrtsberichten
ganz allgemein in die Nichtberücksichtigung der - von Ort zu Ort sich
ändernden - magnetischen Deklination - den unbekannten magnetischen
Bedingungen - zu setzen ist. Wie aber macht man sich die von Ort zu Ort
unterschiedlichen Abweichungen der Magnetnadel vom geographischen Nordpol
plausibel? Am besten so, daß man den "wahren Punkt" herausfindet,
auf den die lingulae nauticae verweisen.
"Wo dieser Punkt zu suchen ist, nach
dem die Magnetnadel so fleißig strebt, das will ich jetzt - so weit
ich vermag - Euer Hochwürden allgemein beschreiben. Zunächst
bestätigt die Erfahrung, daß die Magnetnadel [das nautische
Zünglein] an ein und demselben Ort nach ein und demselben Punkt vom
Himmelsnordpol abweicht. Am Himmel kann dieser Punkt also
nicht gelegen sein, denn da jeder Punkt am Himmel - mit Ausnahme des Himmelspoles
- an einer drehenden Bewegung teilhat, müßte die Nadel beim
täglichen Umschwung eines derartigen Punktes sich bald nach der einen,
bald nach der anderen Seite wenden, und somit wechselnde Deklinationen
zeigen, was der Erfahrung widerspricht. Demnach muß jener Punkt
auf der fest ruhenden Erde zu suchen sein.“
.
Hatte er sich 1546 auf die Lagen
von Walcheren und Danzig eingelassen,
"Nachdem ich den Längenunterschied
zwischen der seeländischen Insel Walcheren und Danzig
genau berechnet und die dazwischenliegenden Küsten nach den Angaben
der Seeleute auf das sorgfältigste gezeichnet habe, finde ich, daß
Danzig
hiernach ungefähr 1° nördlicher liegt als seine gegenwärtige
Lage angenommen wird, woraus ich schließe, daß die Magnetnadel
in Danzig etwa 5° mehr vom wahren Nordpol abweicht als in Walcheren.
In der Gegend dieser Insel beträgt, wie ich weiß, die östliche
Mißweisung 9°. In Danzig wird die Nadel also 14° abweichen.
Legt man nun durch beide Orte Großkreise, die mit den Meridianen
genau diese Winkel haben, so ergibt sich, daß ihr Durchschnittspunkt
auf etwa 79°N und 168°O fällt, so daß
hier also der magnetische Pol liegen muß."
Vgl. Hellmann [Rara]
S.
67-68), ebenso in der Lebensdarstellung das Jahr 1546.
Da Mercator 1546 weder die
Koordinaten von Walcheren (?Middelburg) noch von Danzig anzeigt,
gehe ich beim Nachrechnen von den Koordinaten von 1569
bezüglich der Kapverdischen Insel Bonavista aus: Walcheren
= (26°48'O|51°36'N), Danzig = (43°30'O|54°48'N).
Das Ergebnis führt mit den angegebenen Deklinationen zu einer Breite
von 78°20'N in guter Übereinstimmung
mit Mercators Angabe von 79°N.
so läßt er sich nun auf die Lagen von Corvo und Löwen
ein:
Das Resultat der Rechnung:
Der '54er Magnetpol' liegt in einer Breite von 77°7'
auf
dem Meridian von Corvo..
Da Mercator aber nicht rechnete sondern zeichnete, kann seine Angabe
(73°2' - wenn kein Abschreibefehler vorliegt: 3 anstelle
von
7) und d.h. ihre Abweichung durch Meßfehler an einer vielleicht
zu kleinen Zeichnung verständlich gemacht werden.
In einer Zeichnung (Kugelradius = 16 cm) sind auch (meine)
0,2° nur geschätzte: Konstruiert man durch Umlegung beider
Großkreise den Polpunkt, so erhält man etwa 77°12'.
Josef Müller-Reinhard gab 1913
als Ergebnis seiner Rechnungen "ungefähr 77°"
an (Averdunk S.122).
1569 fixiert er ein weiteres
Mal die Lage des Magnetischen Pols; er geht dann allerdings nicht mehr
von der Azoreninsel Corvo sondern von den Kapverdischen Inseln
aus:
"Polus magnetis respectu insularum capitis viridis."
In der Legende De longitudinum geographicarum
initio et polo magnetis der Weltkarte heißt es u.a.:
"Franziskus von Dieppe, ein sehr
erfahrener Kapitän, bezeugt, daß die beweglichen (magnetischen)
Nadeln, von der magnetischen Kraft beinflußt, bei den Kapverdischen
Inseln, bei Bonavista und der Insel Maio direkt auf den
Erdpol zeigen.Damit stimmen diejenigen eng überein, die sagen, daß
dies [auch] auf Terceira oder S.Maria (das sind Inseln der
Azoren) geschehe. Einige wenige vermuten, daß sich dies ebenso auf
der westlichsten dieser Inseln mit dem Namen Corvo zutrage."
"Und da anderswo die Magnetnadel mehr oder weniger
vom Pol abweicht und es irgendeinen speziellen Pol geben muß, auf
den sich die Magnetnadeln aus allen Teilen der Welt beziehen, habe ich
ihm den Ort zugewiesen, an dem ich ihn gekennzeichnet habe, zu dem ich
die magnetischen Abweichungen von Regensburg benutzt habe."
Leider gibt er die | seine Mißweisung von Regensburg nicht
an.
Die Kapverdischen Inseln liegen auf dem Erdglobus etwa 6° östlich
von
Corvo.
Von 1546 bis 1569
zusammengestellt:
1546
Nulllinie durch Bonavista (1569):
A = Walcheren C = Danzig
Rechnung: 78°20' N Mercator: 79° N
|
1554
A = Corvo C = Löwen
Rechnung: 77°7' Zeichnung (heute): 77° 12'
Mercator: : 73°2'
|
1569
mit Bezug auf Corvo: (173°48'O | 77°N)
77° = die berechnete '54er Breite (Mercator:
73°2')
!
|
1569
mit Bezug auf S.Maria: (180°O
| 73°12'N )
73°2' = die Breite von 1554 !
|
Da die Deklination von Regensburg nicht angegeben wird, könnte
man sich
a) auf die bisher gemachten Angaben Mercators bezüglich
Löwen,
Walcheren
und Danzig einlassen: Mittelt man die drei Ergebnisse, so erhält
man in guter Übereinstimmung mit Mercators Werten von 1569
| 1954 eine Magnetpolbreite von 73°45'.
Geht man dagegen von der Annahme
b) einer Deklination von ?12°O
im Regensburg = (36,6°O|48,8°N) der damaligen
Zeit aus, so liegt der Magnetische (Süd)Pol mit Bezug auf die Kapverdischen
Inseln in einer Breite von 73°20' auf Mercators 180.Längengrad
-
in bemerkenswerter Übereinstimmung mit Gerhard Mercators
'69er
| '54er Datum. Hätte damals in
Regensburg
eine Deklination von 10° O vorgelegen,
so fiele der Polpunkt in die Breite 76°39'.
Interessant scheint mir zu sein, daß John
Gregorie (1607-1649),
"Master of Arts of Christ-Church in Oxon" noch 1649
in seiner Abhandlung Beschreibung und Gebrauch
des Erdglobus die Diskussion über
die Festlegung des "Hauptmeridians" mehrfach aufnimmt:
"Concerning
the Difference of Geographers in the placing of their Great Meridian, and
the Causses pretending thereto.
... This Coincidencie of the Magnetical
Meridian with that of the World, Som of them will have to bee in the Isles
Corvo, and Flores, the most Western: Others in S. Michaël, and S.
Marie, the more Eastern of the Azores. 6 'Tis true indeed that the Variation
is less in these Isles, then in som other Places, yet it is by experience
found, that the Needle in Corvo North-Westeth 4 Degrees: in S. Michaël
it NorthEasteth 6 Degrees: And therefore the Great Meridian should rather
have been drawn through Fayal, where the Variation is but 3 Degrees to
the East; Or especially through the Cape of good hope, where the Needle
precisely pointeth to the True North without any Variation at all by a
River side there, which therefore the Portugals have called Rio de las
Agulias, The River of the Needles.
Es ist schon interessant, welche
Diskussion Gerhard Mercator mit seiner Legende 1569
über den Magnetpol losgetreten hat.
Die Erfahrungen - von denen Gregorie
im Folgenden spricht - zeigen ihm, daß die Deklination an einem
(festen) Ort - überhaupt und nicht nur "at
Limehouse near London" - veränderlich
ist. Diese Veränderlichkeit nötigt Gregorie (1649)
daher den folgenden - wenn gleich substantiell - falschen Schluß
ab (Sperrung von mir):
But which is more, the Magnetical Needle hath
no certain Pole in the Earth at all, and under the verie same Meridian
is found to varie in som places but 3, or 4 Degrees; in other 17, and more;
and which is wors (if it bee true) the Variation it self hath been lately
charged upon with a verie strange and secret inconstancie by the Professor
in Astronomie of Gresham-College. Hee saith that the Variation of the Needle
at Limehous near London, which Mr Burrows found to bee 11 Degrees,
15 Minutes, in the year 1580: M Gunter in the year 1622 found it
to bee but 6 Degrees 13 Minutes. But Hee himself in the year 1634
found it to bee but 4 Degrees, or verie little more; which in the space
of 54 years is a difference of 7 Degrees to the Less. So little reason
is there why the Greek Meridian should give place to the Magnetical, besides
the great confusion which must needs follow, as it hath.
Was die von Bur(r)ough 1581
angemahnten "considerations of the Variation" anbetrifft, so mußte
die Seefahrt immerhin noch bis zum Jahre 1702
zuwarten - denn dann erst zeichnete Edmund Halley in seine
Tabula
Nautica erste Isogonen: -
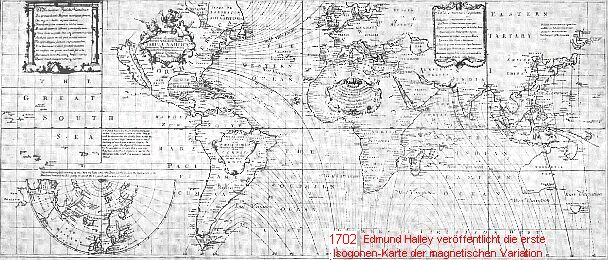 , ,
und - nicht nur - die Längenbestimmung auf See
ließ selbst zu diesem Zeitpunkt noch zu wünschen übrig.
What Cours is to bee taken with this Varietie
of Meridians, and how followed, or neglected by the Geographer.
... That the Great Meridian by the most
Ancient Greek Geographers was made to pass through the Fortunate Islands,
now called The Canaries. That from thence it was translated by the Arabians
to the uttermost Point of the Western-Shore. That our own Geographers removed
it into the Azores placing it som of them in S. Michaël, others in
Corvo. That the Best of them brought it back to the Canaries again, and
drew it upon the Pico in Tenariffe; The same, or thought to bee the same
with Ptolomie's Junonia. That the Difference of Longitude from El
Pico to the Arabick Meridian is 10 Degrees more East according to Abulfeda
the Prince. From Pico to the Isle of S. Michaël 9 Degrees. From Pico
to Corvo 15, and both so much more West. And such, or such a Meridian I
mean to follow.
To this very purpose the same Abulfeda
in the Introduction to his Geographie. It is received by Tradition (saith
hee) that the Inhabited Earth begineth at the West in the Fortunate Isles,
as they are called, and lying waste as now. From these Islands som take
the Begining of Longitude. Others from the Western Shore. The Difference
of Longitude is 10 Degrees accounted in the Equator, &c. As for the
Longitudes reckoned in this Book, they are all taken from the Shores of
the Western Oceän, and therefore they are 10 Degrees short of those
which are taken from the Fortunate Isles, &c.
... Mr Carew in his Survey of Cornwall
setteth down that Shire in the Longitude of 6 Degrees (I believ hee mean't
16) as most men account. But what doe's hee mean by that; or what manner
of account is it which most men use in this case? Norden in the Introduction
to his Speculum Britanniæ saith, That the Center of this Land, which
hee taketh to bee about Titburie Castle in Stafford-Shire is 21 Degrees
and 28 Minutes of Longitude. But from what Meridian all this while? for
the Longitude may bee manie Degrees more, or less, or just so much as hee
saith, and yet all may bee true.
... Mr Speed more particularly professeth
to follow Mercator; as in assigning the Longitude of Oxford, hee saith,
that it is distant from the West 19 Degrees 20 Minutes by Mercator's Measure.
So M. William Burton in the Description of Leicester-Shire. But how are
wee the wiser for this? Mercator's Measure was not the same, for in his
Globe dedicated to the Lord Granvella the great Meridian passeth through
the Canaries; but in his great Map through the Azores. M. Gabriel Richardson
in the State of Europe yet more distinctly telleth his Reader, That the
Longitudes in his book shall bee taken from that Meridian, which passeth
through the Azores. But whether from that in S. Michaël, or from the
other in Corvo is not set down, and yet the Difference is 7 Degrees, and
more: But hear lastly the Kingdom's Geographer in the Preface to his Britannia.
‘At
insimulabunt jam Mathematici & in crimen vocabunt quasi in Geographicis
Latitudinis & Longitudinis Dimensionibus toto Cœlo aberrârim.
Audi quæso: Tabulas Astronomicas, novas, antiquas, manuscriptas,
Oxonienses, Cantabrigienses, Regis Henrici Quinti diligenter contuli. In
Latitudine à Ptolemeo plurimion discrepant inter se ferè
conspirant: nec tamen Terram è suo Centro dimotam esse cum Stadio
existimo. His igitur usus sum, In Longitudine autem nullus consensus, concentus
nullus. Quid igitur facerem? Cum Recentiores perpendiculum navigatoria
pyxide Magnete illitum inter Azores insulas rectà Polum Borealem
respicere deprehenderim, indè Longitudinis Principium tanquam à
Primo Meridiano cum illis dixi quam nec ubique leptomer permensus
sum.’ So the Learned Cambden. Where note by the waie, that if the Translator
hath rendered the Book no better then hee hath this Claus of the Preface,
the best cours will bee for those that can, to read it in the Latine. The
Autor's meaning I think was this.
... But I finde by the Longitudes that Mercator
was the Man that set up all these for Geographers.
Mercator first of all kept himself to
the Greek Meridian, as, Appian, Gemma Frisius, Maginus,
and others; but understanding by Francis of Deip, an experienced
Mariner, that the Compass had no Variation in the Islands of Capo Verde.
And by others, that it had very little in Tercera, and S. Marie of the
Azores, but not anie at all in the Isle Corvo, that hee might go a mean
waie to work, and complie with the Common Meridian of the World (as hee
took it to bee). Hee made his Great Meridian to pass (as himself saith)
betwixt the Isles of Capo Verde and the Azores; that is, Through the Isles
of S. Michaël and S. Marie, which was afterwards taken for Example
by Plancius,
Saunderson, and the common sort of others, so
that little or no notice at all was taken of the Meridian by Corvo, no
not by those of the biggest expectation, as M. Carpenter, M.
Camden, M. Speed, and the rest; although this also was the known
Meridian of som Globes of the very same Times; and before that, that is,
before they had set their last hand to their Descriptions. And 'tis no
mervail, for Mercator's Longitudes were more exactly accounted then
before, and therefore they might well take his Meridian along with them.
And 'twas not amiss to go by the most received, but then they should have
said so, and withall, have set down the three severall Meridians at least,
and the difference of Longitude betwixt them; and all this with more distinction
then so, that another man should com after them to tell themselvs what
Meridian they went by.
And thus much of the First, or Great Meridian."
[3] [5]Breitengrad des Ortes
wissen | auf den Breitengrad
Die Angabe der Breite ist erforderlich, damit der Meridianring korrekt
auf die Polhöhe eingestellt werden kann. Erst dann können alle
weiteren Überlegungen angestellt werden. (Satz von der Polhöhe.)
Ein Verfahren, den "wahren" Meridian mithilfe des Kompaß zu ermitteln,
finden wir bei Peter Apian Cosmographus
Liber (1524): Alia
et iusta lineae meridianae inventio, col.51:
bzw. Cosmographia (1540)
f.XXIVv Prima Pars: Sequitur alia &
exacta linea meridianae inventio:
Mercator ersetzt am Globus das Lineal durch den Höhenkreis.
(Siehe die folgenden Anmerkung.)
[4]Meßschenkel des Höhenquadranten
Als latus fiducialis (Meßschenkel) des
Höhenquadranten ist der Schenkel MC
zu verstehen.
[6]Korrektur
Gerhard Mercator korrigiert - wohl als erster Geograph - die
Vorstellungen des Claudius Ptolemäus inbezug auf die Längenausdehnung
des Mittelmeeres und damit Europas.
Bei Ptolemäus erstreckte sich das Mittelmeer über
62° - wie bei Gerhard Mercator
(a) 1536 in seiner Doppelt-herzförmigen
Weltkarte und
(b) im "wiederhergestellten" Ptolemäus
von 1578 /
84:
1541 beginnt auf seinem Globus
eine vorsichtige Korrektur: aus 62° werden 58°;
- die (weitere) Korrektur beginnt mit den Vorbereitungen zur Europa-Karte,
die parallel zu seinen Untersuchungen zum "wahren" Nullmeridian verlaufen.
In ihr hat das Mittelmeerbecken (1554 /
1572)
noch eine Ausdehnung von 52.07°:
1569 mißt das Mittelmeerbecken
schließlich 51°18'.
Daß dennoch nicht die "heutigen" und damals vielleicht bestmöglichen
Ausmaße erzielt wurden, liegt wohl daran, daß Mercator
?offenbar keine Portolane des Zeitalters bekannt gewesen sind - wie ich
schon 1994 vermutete..
Untersuchungen an der Universität Essen
(Vermessungswesen | Kartographie : Prof. Dr.-Ing. Peter Mesenburg)
im Jahre 2001 bestätigen meine
Vermutung und machen den (bekannten) Unterschied kartometrisch fest:
.
Für das Mittelmeer ergibt sich nach Mesenburg
ein Fehler von ungefähr 1.3 (Mercator) : 1 (heutigentags). Messen
wir von Gibraltar (Säulen des Herkules) bis zum Strand von Antakya,
so erhalten wir heutigentags ein Aufmaß von 41°13'; Mercator
hatte in ad usum noch die w.o.a. 51°18'
(1 : 1.25).
Die Ausführungen hier (1552ff)
zeigen, daß das Studium der Quellen seiner - kommenden - Europa-Karte
schon weit fortgeschritten ist. Und
1552ff
befindet er sich immer noch auf der Suche nach der Lage des "wahren" Nullmeridians:
1552
geht er durch Corvo, 1569 durch
Bona
Vista. Die magnetischen Isogonen hält er zu diesem Zeitpunkt -
wie auch später noch - für Großkreise einer kugelförmigen
Erde. Ein Umdenken ist wohl wegen der fehlenden allgemeinen Erfahrung nie
erfolgt. Und nur unter dieser Voraussetzung lassen sich seine Ausführungen
an den Kaiser verstehen.
.
Daß er sich bei seinen "magnetischen" Überlegungen
- sit venia verbo - nicht in schlechter Gesellschaft befand, beweisen die
sehr viel späteren Experimente und nachfolgenden Theorien
De
magnete, magneticisque corporibus, et de magno magnete tellure
(1600) von
William Gilbert (1544-1603),
welcher dieser allerdings nicht so sehr der Deklination als
vielmehr der Inklination des Magneten widmet. Wie Mercator
- die Linien gleicher Deklination sind Großkreise -
glaubt Gilbert, daß es eine umkehrbar-eindeutige Abbildung
der Bewegung der Inklinationen auf die Folge
der Breitengrade gibt (liber V)
:
...this movement is in truth not a dipping movement, but really
a revolution movement, and it describes an arc of revolution proportioned
to the arc auf latitude. (Übertragung von P.F.Mottelay;
die Unterstreichungen von mir.) Wie Gerhard Mercator kann er die
von ihm angedachte Funktion zwar
nicht arithmetisch wohl aber geometrisch
darstellen. Und es ist wie bei Mercator : es handelt sich um eine
spirall line.
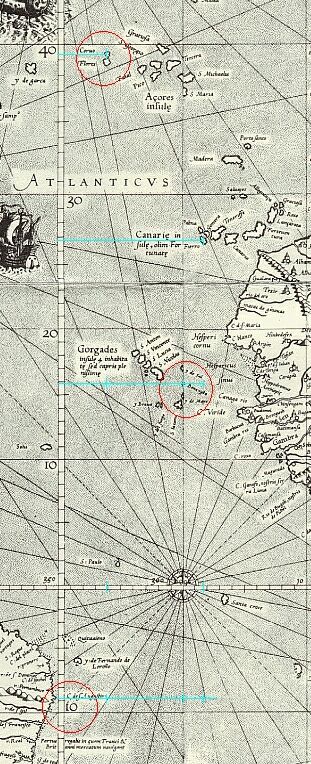
[7]durch die Insel Corvo
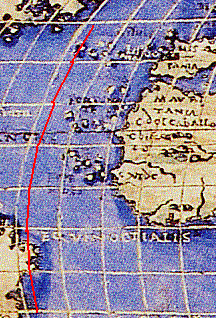
Franco Roselli 1508
Der Meridian von Corvo ist rot eingezeichnet. |
 |
[8]nach Süden
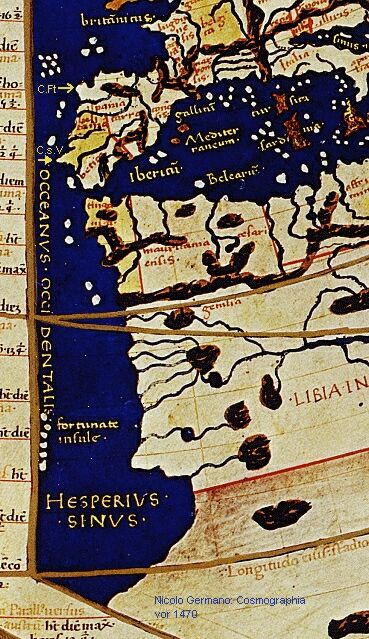
Die Geographia des Ptolemäus
wurde schon 1406 von Jacopo Angelo
ins Lateinische als "Cosmographia" übersetzt, und um
1415 fügten Francesco Lapacino
und
Domenico
di Leonardo Boninsegno die Kartentafeln dem Werk hinzu. |
Im Cod. lat.V. F. 32 zu Venedig
findet sich eine dem Nicolaus Germanus zugeschriebene Weltkarte
in der Tradition des Ptolemäus, die die Argumente Gerhard
Mercators illustriert
Kap Finisterre (C.Ft.) liegt auf 5.1/2° (Ferro)
Kap San Vicente (C.s.V.) liegt auf 3° (Ferro)
Entsprechende Lagebeziehungen finden wir auch noch in der Weltkarte
Waldseemüllers
von 1507.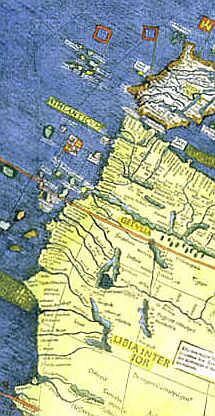 |
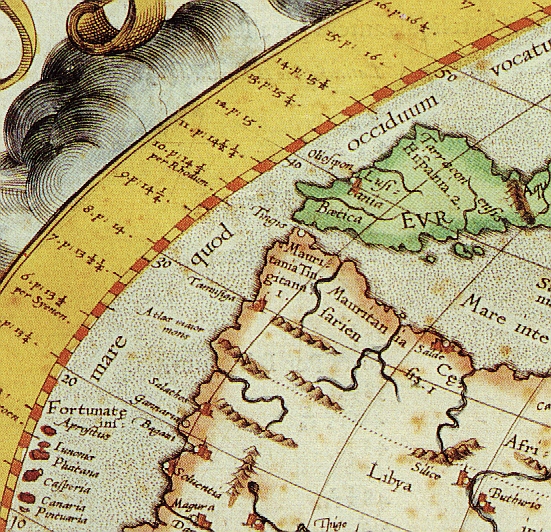
In seiner Rekonstruktion "im Geiste des Ptolemäus" treffen
seine Argumente noch 1578/84 zu.
Allerdings: Spanien erstreckt sich nicht mehr über 20 Längengrade.
[9]auf 20° hinzieht
[10]Ptolemäus
Da die Vorlagen Mercators nicht auffindbar sind, vergleiche
ich seine Angaben von 1554 mit denen
auf der Karte ad usum navigantium.
Die Angaben aus dem Atlaswerk von
1595
:: Rumold: Globularkarte,
Michael:
Amerika
:: entsprechen den Lagen von
1569,
da beide sie der Karte ad usum navigantium
abgezogen haben.
 |
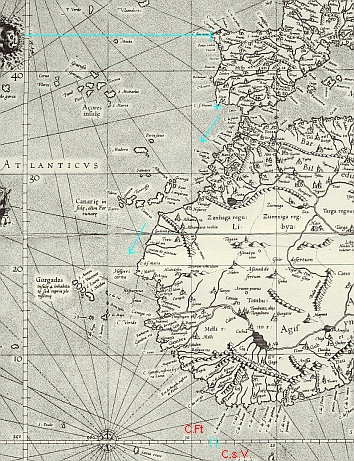
Die Routen vor Portugal verlaufen in südlicher Richtung, die an
der nordwestlichen Küste Afrikas - oberhalb des Äquators - in
südwestlicher, südlicher und südöstlicher Richtung.
Bezüglich des "wahren" Meridians durch Bona Vista macht
ad
usum navigantium (1569)
folgende Angaben:
|
1554 |
1569 |
| Ferro |
0° |
1.8° |
| Corvo |
349.5° |
354° |
| Kap Finisterre |
5.5° |
12.3° |
| Kap San Vicente |
3° |
13° |
| Kap San Agostino |
348° |
349.8° |
| Größe Spaniens |
20° |
14° |
|
11]index horarius
Der index horarius besteht aus
einem mit dem Ortsmeridian (am Nordpol) festverbundenen "Stundenkreis"
mit einer 2x12h-Einteilung und dem mit der Weltachse - d.h. mit dem Äquatoring
- festverknüpften "Stundenzeiger", so daß dieser den Winkel
zwischen dem Ortsmeridian und dem 'Stundenkreis' eines Gestirns - sozusagen
den "Fortschritt" des Gestirns seit seiner "oberen Kulmination" bzw. die
Drehung des Äquators aus dem Ortsmeridian heraus - in Stunden,
Minuten und Sekunden - zu messen in der Lage ist.
[12]gnomonis sphaerici

|
Wie
Mercator sich den gnomo sphaericus wohl
gedacht hat, geht aus der Titelei der Abhandlung
des
Gemma Phrisius De principiis astronomiae et
Cosmographiae hervor:
Der Kompaß, das Lot und der "sphärische" stylus sind
für den Gebrauch des Gemma'schen Erdglobus / des Mercator'schen
Doppelglobus unabdingbare Hilfsmittel. |
[13] arcturus
Im Sternbild Bootes (griech. bowthV - lat.
(bei Mercator:) bubulcus = Ochsentreiber) finden wir den (hellen)
Stern - nach Mercator: 1 Ordnung) Arcturus (RA= 14h15m45.51s
| DE=19°09'10.41" | Epoche 2000) = alpha bootis.
Im Sternbild Fuhrmann (lat. auriga) finden wir den (hellen) Stern
(nach
Mercator: 1.Ordnung)
Hircus = Ziegenbock = Capella
(RA=5h16m55.12s | DE= 45°49'13.71"
| Epoche 2000).
.
Es ist bei der Betrachtung der Sternbilder (nach Mercator)
zu beachten, daß nahezu alle menschlichen Figuren-Sternbilder in
der "Globussicht" von einem außerhalb der Himmelskugel liegenden
Standpunkt aus (auf der konvexen Himmelskugel) dargestellt sind - nicht
aber von einem Betrachter aus, der die Sternbilder auf einer (konkav-gesehenen)
Hohlkugel - sozusagen mit korrektem Blick - aufgetragen sieht:
:
Der Unterschied zwischen der Globus- und der Himmelsansicht
ist beim Vergleich der vorstehenden Mercator-Bilder mit einer "teleskopischen
Momentaufnahme" gut erkennbar (Epoche 1550
- UTC: 16:33:24):
Die Längendifferenz zwischen den Sternen des Ptolemäus
und denen des Himmelsglobus beträgt rund 21°. Vermutlich hat er
den Wert von 20°55' den Revolutionen
des Copernicus entnommen
 Daß
Gerhard
Mercator äquatoriale Koordinaten aus den Sternentafeln des Copernicus1543
abgeleitet hat, halte ich für sehr unwahrscheinlich, denn schließlich
enthalten die Tafeln des
Copernicus wie die des Ptolemäus
zodiakal-bestimmte Koordinaten, die Mercator in äquatoriale
hätte (a)
umrechnen - mit Hilfe
einer rechnenden Mathematik, die Mercator - soweit heute bekannt
- nicht beherrschte, bzw. (b) mühsam mit Hilfe der entsprechenden
Tafeln der Revolutionen 31r, 31v gemäß
Lehrsatz
IV Buch I 21r ff hätte aufarbeiten müssen - ein Unternehmen,
das erst Erasmus Reinhold auf sich genommen hat. Für sehr wahrscheinlich
halte ich, daß er - im Besitze des Almagest - der konstruktiven Methode
des Ptolemäus gefolgt ist: Daß
Gerhard
Mercator äquatoriale Koordinaten aus den Sternentafeln des Copernicus1543
abgeleitet hat, halte ich für sehr unwahrscheinlich, denn schließlich
enthalten die Tafeln des
Copernicus wie die des Ptolemäus
zodiakal-bestimmte Koordinaten, die Mercator in äquatoriale
hätte (a)
umrechnen - mit Hilfe
einer rechnenden Mathematik, die Mercator - soweit heute bekannt
- nicht beherrschte, bzw. (b) mühsam mit Hilfe der entsprechenden
Tafeln der Revolutionen 31r, 31v gemäß
Lehrsatz
IV Buch I 21r ff hätte aufarbeiten müssen - ein Unternehmen,
das erst Erasmus Reinhold auf sich genommen hat. Für sehr wahrscheinlich
halte ich, daß er - im Besitze des Almagest - der konstruktiven Methode
des Ptolemäus gefolgt ist:
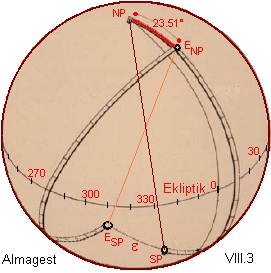 Wenn
er seinen Himmelsglobus aber nach der Methode des
Ptolemäus konstruiert
hat (Almagest
VIII 3), ist es hinwiedrum
unwahrscheinlich, daß er die Tafeln des Copernicus benutzt
hat (wie Elly Dekker1992
unterstellt). Frau Dekker meint, er habe mehrere Verzeichnisse
benutzt; D.J.Warner
führt Tafeln an, die - höchst - wahrscheinlich (nach Ausweis
des Katalogs von 1604)
nicht im Besitze
Gerhard Mercators gewesen sind. Beide glauben eine
Präzessionsdrift von
20°55' seit Ptolemäus
ausmachen zu können. Wenn
er seinen Himmelsglobus aber nach der Methode des
Ptolemäus konstruiert
hat (Almagest
VIII 3), ist es hinwiedrum
unwahrscheinlich, daß er die Tafeln des Copernicus benutzt
hat (wie Elly Dekker1992
unterstellt). Frau Dekker meint, er habe mehrere Verzeichnisse
benutzt; D.J.Warner
führt Tafeln an, die - höchst - wahrscheinlich (nach Ausweis
des Katalogs von 1604)
nicht im Besitze
Gerhard Mercators gewesen sind. Beide glauben eine
Präzessionsdrift von
20°55' seit Ptolemäus
ausmachen zu können.
Ohne sonstigen Verweis kann diese Zahl nur den Revolutionen
des Copernicus entnommen worden sein: III.12 78r, und in der Tat
ist am Globus 1551 empirisch - d.h. in den Grenzen möglicher Meßgenauigkeiten
- nachzuvollziehen, daß die Längenangaben bei Gerhard Mercator
denen des Ptolemäus entsprechen - vermehrt um 20°55' ,
rd 21°.
Devorah J. Warner schreibt The
sky explored S.174, daß "Mercator's
star positions agree with those for epoch 1550 published by Johannes Schöner
in his Globi Stelliferi, sive Sphaera Stellatum (Nuremberg
1551)". Sie glaubt, daß Schöner
seine aus den Beobachtungen Bernhard Walthers (1430
- 1504)
abgeleitet habe, die dieser angestellt habe, weil Regiomontan (1436
- 1468)
auf etliche (akkumulierte) Fehler der Alphonsinischen
Tafeln aufmerksam gemacht habe. Es ist
aber sicher - die Herausgabe des Himmelsglobus
hat gewiß eine ein- bis zweijährige Vorlaufzeit gehabt - , daß
Gerhard Mercator Schöners Sterntabellen nicht benutzt hat
Die 1604
erwähnte Ausgabe Cl. Ptolemaei opera
excepta Geographia (cum
quibusdam notis marginalisbus Gerardi Mercatoris)
Bas[el]
l541
habe ich - bis dato - nicht auffinden können, - wohl aber die von
Simon
Grynaeus besorgte Ausgabe Magnae constructionis,
id est, perfectae coelestium motuum pertractattionis,
lib. XIII, Basileae, ap.Jo.Walder, 1538,
fol. (Manitius: editio princeps).
Die Ausgabe des Almagest
von 1528
(Warner) habe ich - bis dato - nicht aufgefunden.
Rectascension:
a = 24,26° = 1,617h = 1h37m2s
Deklination:
d = 7,99° = 7°59'. |
UMRECHNUNG
(4) aus dem Zodiakalsystem ins Äquatorialsystem
Gegeben (l | b) .
Gesucht (a | d)
.
e = Schiefe der Ekliptik
Führen wir die Hilfsgröße Q ein :
Q = arctan [sin (l) / tan (b)]
a = arctan [tan (l)
· sin (Q - e) / sin (Q)]
Achtung: a und l
müssen im selben Quadranten liegen!
d = arctan [sin (a) / tan (Q - e)]
--------------------------------------------------------
Rechnen wir ein historisches Beispiel durch:
Peter Apian berechnete 1546
im Feldlager Karls V. die Saturnkoordinaten für den Geburtstag
des Kaisers am 25. Februar 1500:
l = 25°39'
b = -2° = 2°S
Für Q ergibt die Rechnung: Q = -85,39°.
Damit erhält man einerseits / andererseits:
|
"In sinistro humero fulgens quam uocant capellam":
Die (heutzutage) berechneten Koordinaten a
Aurigae sind a = 4H 43M 42.1S | d
= 45° 24'12''.
[14]antarcticum
Raemdonck: antarticum.
|